Elektromagnetite tõmbejõud

Jõud, millega elektromagnet tõmbab ferromagnetilisi materjale, sõltub magnetvoost F või samaväärselt induktsioonist B ja elektromagneti S ristlõike pindalast.

Elektromagneti survejõud määratakse valemiga

F = 40550 ∙ B ^ 2 ∙ S,

kus F on elektromagneti survejõud, kg (jõudu mõõdetakse ka njuutonites, 1 kg = 9,81 N või 1 N = 0,102 kg); B — induktsioon, T; S on elektromagneti ristlõikepindala, m2.

Näited

1. Segisti elektromagnet on magnetahel (joonis 1). Kui suur on hobuseraua-kraana elektromagneti tõstejõud, kui magnetinduktsioon on B = 1 T ja elektromagneti iga pooluse ristlõikepindala on S = 0,02 m2 (joonis 1, b)? Jäta tähelepanuta elektromagneti ja armatuuri vahelise pilu mõju.

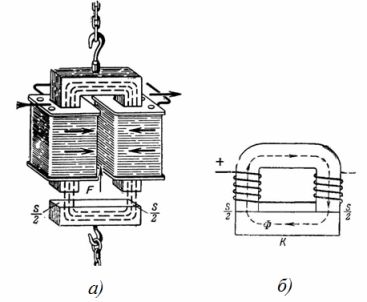
Riis. 1. Tõste elektromagnet

F = 40550 ∙ B ^ 2 ∙ S; F = 40550 ∙ 1 ^ 2 ∙ 2 ∙ 0,02 = 1622 kg.

2. Ringikujulise terasest elektromagneti mõõtmed on näidatud joonisel fig. 2, a ja b. Elektromagneti tõstejõud on 3 T. Määrake elektromagneti südamiku ristlõikepindala n. p ja pooli keerdude arv magnetiseerimisvoolul I = 0,5 A.

Riis. 2. Ümmargune elektromagnet

Magnetvoog läbib ringikujulist sisemist südamikku ja naaseb läbi silindrilise korpuse. Südamiku Sc ja korpuse Sk ristlõikepindalad on ligikaudu samad, seetõttu on induktsiooni väärtused südamikus ja korpuses praktiliselt samad:

Sc = (π ∙ 40 ^ 2) / 4 = (3,14 ∙ 1600) / 4 = 1256 cm2 = 0,1256 m2,

Sk = ((72 ^ 2-60 ^ 2) ∙ π) / 4 = 3,14 / 4 ∙ (5184-3600) = 1243,5 cm2 = 0,12435 m2;

S = Sc + Sk = 0,24995 m2 ≈0,25 m2.

Elektromagnetis nõutav induktsioon määratakse valemiga F = 40550 ∙ B ^ 2 ∙ S,

kus B = √ (F / (40550 ∙ S)) = √ (3000 / (40550 ∙ 0,25)) = 0,5475 T.

Selle induktsiooni pinge leitakse valuterase magnetiseerimiskõveralt:

H = 180 A/m.

Väljajoone keskmine pikkus (joon. 2, b) lav = 2 ∙ (20 + 23) = 86 cm = 0,86 m.

Magnetiseeriv jõud I ∙ ω = H ∙ lav = 180 ∙ 0,86 = 154,8 Av; I = (I ∙ ω) / I = 154,8 / 0,5 = 310 A.

Tegelikult n. s, see tähendab vool ja pöörete arv, peavad olema mitu korda suuremad, kuna elektromagneti ja armatuuri vahel on vältimatu õhupilu, mis suurendab oluliselt magnetahela magnettakistust. Seetõttu tuleb elektromagnetite arvutamisel arvestada õhuvahega.

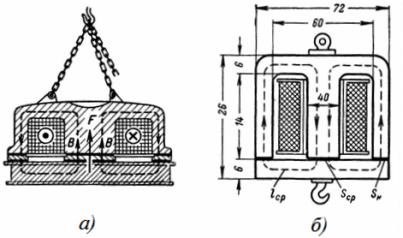
3. Segisti elektromagneti mähis on 1350 pöördega, läbib vool I = 12 A. Elektromagneti mõõtmed on näidatud joonisel fig. 3. Millise raskuse tõstab elektromagnet 1 cm kaugusel armatuurist ja millist raskust suudab see peale gravitatsiooni vastu pidada?

Riis. 3. Elektromagnetiline mähis

Suurem osa N.-st, mille I ∙ ω, kulub magnetvoo juhtimiseks läbi õhupilu: I ∙ ω≈Hδ ∙ 2 ∙ δ.

Magnetiseeriv jõud I ∙ ω = 12 ∙ 1350 = 16200 A.

Kuna H ∙ δ = 8 ∙ 10 ^ 5 ∙ B, siis Hδ ∙ 2 ∙ δ = 8 ∙ 10 ^ 5 ∙ B ∙ 0,02.

Seetõttu 16200 = 8 ∙ 10 ^ 5 ∙ B ∙ 0,02, s.o. B = 1,012T.

Eeldame, et induktsioon on B = 1 T, kuna osa n-st. c) I ∙ ω kulutatakse terase magnetvoo juhtimiseks.

Kontrollime seda arvutust valemiga I ∙ ω = Hδ ∙ 2 ∙ δ + Hс ∙ lс.

Magnetjoone keskmine pikkus on: lav = 2 ∙ (7 + 15) = 44 cm = 0,44 m.

Intensiivsus Hc B = 1 T (10000 Gs) juures määratakse magnetiseerimiskõvera järgi:

Hc = 260 A / m. I ∙ ω = 0,8 ∙ B ∙ 2 + 2,6 ∙ 44 = 1,6 ∙ 10000 + 114,4 = 16114 Av.

Magnetiseeriv jõud I ∙ ω = 16114 Av, mis tekitab induktsiooni B = 1 T, on praktiliselt võrdne antud n-ga. v. I ∙ ω = 16200 Av.

Südamiku ja koonuse ristlõike kogupindala on: S = 6 ∙ 5 + 2 ∙ 5 ∙ 3 = 0,006 m2.

Elektromagnet tõmbab 1 cm kauguselt ligi F = 40550 ∙ B ^ 2 ∙ S = 40550 ∙ 1 ^ 2 ∙ 0,006 = 243,3 kg laengu.

Kuna pärast armatuuri tõmbamist õhuvahe praktiliselt kaob, talub elektromagnet palju suuremat koormust. Sel juhul kogu n. c) I ∙ ω kulub magnetvoo juhtimiseks ainult terases, seega I ∙ ω = Hс ∙ lс; 16200 = Hs ∙ 44; Hc = 16200/44 = 368 A/cm = 36800 A/m.

Sellise pinge juures on teras praktiliselt küllastunud ja induktsioon selles on ligikaudu 2 T. Elektromagnet tõmbab armatuuri ligi jõuga F = 40550 ∙ B ^ 2 ∙ S = 40550 ∙ 4 ∙ 0,006 = 973 kg.

4. Signaali (vilkuv) relee koosneb ümmarguse südamikuga soomustatud elektromagnetist 1 ja ventiili tüüpi armatuurist 2, mis pärast elektromagnetile voolu andmist tõmbab enda poole ja vabastab vilkuri 3, mis avab signaali numbri (joonis 1). 4).

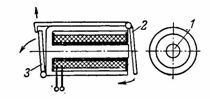
Riis. 4. Soomuselektromagnet

Magnetiseerimistugevus on I ∙ ω = 120 Av, õhuvahe on δ = 0,1 cm ja elektromagneti kogu ristlõikepindala on S = 2 cm2. Hinnake relee tõmbejõudu.

Induktiivsus B määratakse järjestikuste lähendustega, kasutades võrrandit I ∙ ω = Hс ∙ lс + Hδ ∙ 2 ∙ δ.

Olgu n. c) Hc ∙ lc on 15% I ∙ ω, st. 18 Av.

Siis I ∙ ω-Hс ∙ lс = Hδ ∙ 2 ∙ δ; 120-18 = Hδ ∙ 0,2; Hδ = 102 / 0,2 = 510 A / cm = 51000 A / m.

Seega leiame induktsiooni B:

Hδ = 8 ∙ 10 ^ 5 V; B = Hδ / (8 ∙ 10 ^ 5) = 51 000 / (8 ∙ 10 ^ 5) = 0,0637 T.

Pärast väärtuse B asendamist valemis F = 40550 ∙ B ^ 2 ∙ S saame:

F = 40550 ∙ 0,0637 ^ 2 ∙ 0,0002 = 0,0326 kg.

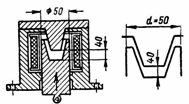
5. DC-piduri solenoidil (joonis 5) on koonilise tõkkega kolvi armatuur. Armatuuri ja südamiku vaheline kaugus on 4 cm Tööläbimõõt (ringikujulise kontaktpinnaga südamikud) d = 50 mm. Armatuur tõmmatakse 50 kg jõuga mähisesse. Keskmise jõujoone lav pikkus = 40 cm Määrake n. lk ja pooli vool, kui on 3000 pööret.

Riis. 5. DC piduri solenoid

Elektromagneti tööosa pindala on võrdne ringi pindalaga, mille läbimõõt on d = 5 cm:

S = (π ∙ d ^ 2) / 4 = 3,14 / 4 ∙ 25 = 19,6 cm2.

Jõu F = 50 kg tekitamiseks vajalik induktsioon B leitakse võrrandist F = 40550 ∙ B ^ 2 ∙ S,

kus B = √ (F / (40550 ∙ S)) = √ (50 / (40550 ∙ 0,00196)) = 0,795 T.

Magnetiseeriv jõud I ∙ ω = Hс ∙ lс + Hδ ∙ δ.

Terase Hc ∙ lc magnetiseerimistugevuse määrame lihtsustatud viisil, tuginedes asjaolule, et see on 15% I ∙ ω:

I ∙ ω = 0,15 ∙ I ∙ ω + Hδ ∙ δ; 0,85 ∙ I ∙ ω = Hδ ∙ δ; 0,85 ∙ I ∙ ω = 8 ∙ 10 ^ 5 ∙ B ∙ δ; I ∙ ω = (8 ∙ 10 ^ 5 ∙ 0,795 ∙ 0,04) / 0,85 = 30 000 keskm.

Magnetiseerimisvool I = (I ∙ ω) / ω = 30000/3000 = 10 A.