Magnetvälja tugevus. Magnetiseeriv jõud

Traadi või mähise ümber on alati elektrivool magnetväli… Püsimagneti magnetväli on põhjustatud elektronide liikumisest nende orbiitidel aatomis.

Magnetvälja iseloomustab selle tugevus. Magnetvälja tugevus H on sarnane mehaanilise tugevusega. See on vektorkogus, see tähendab, et sellel on suurus ja suund.

Magnetvälja ehk magnetit ümbritsevat ruumi võib kujutada täidetuna magnetjoontega, mis arvatakse väljuvad magneti põhjapoolusest ja sisenevad lõunapoolusele (joonis 1). Magnetjoone puutujad näitavad magnetvälja tugevuse suunda.

Magnetväli on tugevam seal, kus magnetjooned on tihedamad (magneti poolustel või voolu juhtiva pooli sees).

Mida suurem on voolutugevus I ja pooli keerdude arv ω, seda suurem on magnetväli juhtme läheduses (või pooli sees).

Magnetvälja H tugevus mis tahes ruumipunktis on seda suurem, mida suurem on korrutis ∙ ω ja mida lühem on magnetjoone pikkus:

H = (I ∙ ω) / l.

Võrrandist järeldub, et magnetvälja tugevuse mõõtmise ühik on amper meetri kohta (A / m).

Iga magnetjoone korral antud ühtlases väljas on korrutised H1 ∙ l1 = H2 ∙ l2 = … = H ∙ l = I ∙ ω võrdsed (joonis 1).

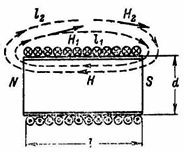
Riis. 1.

Korrutis H ∙ l magnetahelates on sarnane elektriahelate pingega ja seda nimetatakse magnetpingeks ning kogu magnetilise induktsiooniliini pikkuses nimetatakse magnetiseerimisjõuks (ns) Fm: Fm = H ∙ l = I ∙ ω.

Magnetiseerivat jõudu Fm mõõdetakse amprites, kuid tehnilises praktikas kasutatakse nimetuse amper asemel nimetust amper-turn, mis rõhutab, et Fm on võrdeline voolutugevuse ja pöörete arvuga.

Südamikuta silindrilise pooli puhul, mille pikkus on palju suurem selle läbimõõdust (l≫d), võib pooli sees olevat magnetvälja lugeda ühtlaseks, s.t. sama magnetvälja tugevusega H kogu pooli siseruumis (joon. 1). Kuna magnetväli väljaspool sellist mähist on palju nõrgem kui selle sees, võib välise magnetvälja tähelepanuta jätta ja arvutamisel eeldada, et n. c mähis on võrdne pooli sees oleva väljatugevuse korrutisega pooli pikkusega.

Traadi ja voolupooli magnetvälja polaarsus määratakse kardaani reegliga. Kui kardaani edasiliikumine langeb kokku voolu suunaga, siis magnetjoonte suunda näitab kardaani käepideme pöörlemissuund.

Näited

1. Läbi 2000 pöörde pikkuse mähise voolab vool 3 A. Mis on n. v. mähised?

Fm = I ∙ ω = 3 ∙ 2000 = 6000 A. Mähise magnetiseerimistugevus on 6000 ampripööret.

2. 2500 pöördega mähis peaks olema n. lk 10000 A. Milline vool peab seda läbima?

I = Fm / ω = (I ∙ ω) / ω = 10000/2500 = 4 A.

3.Mähist läbib vool I = 2 A. Mitu pööret peab mähises olema, et saada n. küla 8000 A?

ω = Fm / I = (I ∙ ω) / I = 8000/2 = 4000 pööret.

4. 100 pöördega 10 cm pikkuse mähise sees on vaja tagada magnetvälja tugevus H = 4000 A / m. Kui palju voolu peaks mähis kandma?

Pooli magnetiseeriv jõud on Fm = H ∙ l = I ∙ ω. Seetõttu 4000 A / m ∙ 0,1 m = I ∙ 100; I = 400/100 = 4 A.

5. Mähise (solenoidi) läbimõõt on D = 20 mm, pikkus l = 10 cm. Mähis on keritud vasktraadist läbimõõduga d = 0,4 mm. Kui suur on magnetvälja tugevus mähise sees, kui see on sisse lülitatud 4,5 V?

Pöörete arv ilma isolatsiooni paksust arvestamata ω = l∶d = 100∶0,4 = 250 pööret.

Silmuse pikkus π ∙ d = 3,14 ∙ 0,02 m = 0,0628 m.

Mähise pikkus l1 = 250 ∙ 0,0628 m = 15,7 m.

Mähise aktiivne takistus r = ρ ∙ l1 / S = 0,0175 ∙ (4 ∙ 15,7) / (3,14 ∙ 0,16) = 2,2 oomi.

Vool I = U / r = 4,5 / 2,2 = 2,045 A ≈2 A.

Magnetvälja tugevus mähises H = (I ∙ ω) / l = (2 ∙ 250) / 0,1 = 5000 A / m.

6. Määrake magnetvälja tugevus 1, 2, 5 cm kaugusel sirgest traadist, mille kaudu voolab vool I = 100 A.

Kasutame valemit H ∙ l = I ∙ ω.

Sirge traadi korral ω = 1 ja l = 2 ∙ π ∙ r,

kust H = I / (2 ∙ π ∙ r).

H1 = 100 / (2 ∙ 3,14 ∙ 0,01) = 1590 A / m; H2 = 795 A/m; H3 = 318 A/m.