Ühe toiteallikaga hargnemata ja hargnenud lineaarsed elektriahelad

Kui suur hulk passiivseid elemente koos allikaga e. jne. c) moodustavad elektriahela, nende omavahelist ühendamist saab teha erineval viisil. Selliste ühenduste jaoks on järgmised tüüpilised skeemid.

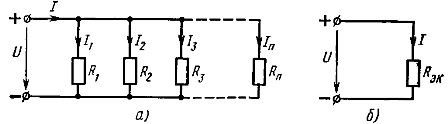
Elementide jadaühendus See on kõige lihtsam ühendus. Selle ühendusega voolab kõigis ahela elementides sama vool. Selle skeemi järgi saab ühendada kas kõik vooluahela passiivsed elemendid ja siis on vooluahel üheahelaline hargnemata (joonis 1., a) või ainult osa mitmeahelalise ahela elementidest ühendatud.

Kui jadamisi on ühendatud n elementi, milles voolab sama vool I, siis on pinge ahela klemmidel võrdne pingelanguste summaga n järjestikku ühendatud elemendis, s.t.

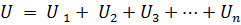
või:

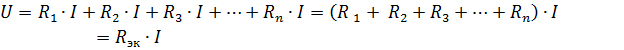
kus Rek on samaväärne vooluahela takistus.

Seetõttu on järjestikku ühendatud passiivsete elementide ekvivalenttakistus võrdne nende elementide takistuste summaga... Elektriskeem (joon.1, a) võib esitada samaväärse vooluringi (joonis 1, b), mis koosneb ühest samaväärse takistusega Rek elemendist

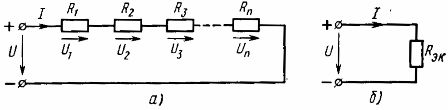
Riis. 1. Lineaarsete elementide jadaühenduse skeem (a) ja sellega samaväärne skeem (b)

Ahela arvutamisel elementidega, mis on järjestikku ühendatud toiteallika etteantud pingega ja elementide takistustega, arvutatakse voolutugevus ahelas Ohmi seaduse järgi:

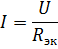
Pingelangus üle k-nda elemendi

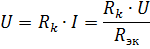
sõltub mitte ainult selle elemendi takistusest, vaid ka samaväärsest takistusest Rek, see tähendab ahela teiste elementide takistusest. See on elementide jadaühenduse oluline puudus. Piiraval juhul, kui ahela mis tahes elemendi takistus võrdub lõpmatusega (avatud vooluring), muutub voolutugevus kõigis ahela elementides nulliks.

Kuna järjestikku ühendamisel on voolutugevus kõigis ahela elementides sama, on elementide pingelanguse suhe võrdne nende elementide takistuste suhtega:

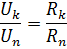
Elementide paralleelühendus - see on ühendus, kus vooluahela kõikidele elementidele rakendatakse sama pinget. Paralleelühenduse skeemi järgi saab ühendada kas kõik ahela passiivsed elemendid (joonis 2, a) või ainult osa neist. Iga paralleelselt ühendatud element moodustab eraldi haru. Seetõttu on joonisel fig. 2, a, kuigi see on lihtne vooluahel (kuna see sisaldab ainult kahte sõlme), on see samal ajal hargnenud.

Riis. 2. Lineaarsete elementide paralleelühenduse skeem (a) ja selle ekvivalentskeem (b)

Igas paralleelses harus vool

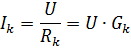
kus Gk on k-nda haru juhtivus.

Alates Kirchhoffi esimene seadus

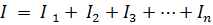
või

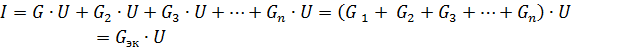
kus Gec on ekvivalentne vooluahela juhtivus.

Seetõttu on passiivsete elementide paralleelsel ühendamisel nende ekvivalentjuhtivus võrdne nende elementide juhtivuste summaga... Ekvivalentjuhtivus on alati suurem kui paralleelsete harude mis tahes osa juhtivus. Ekvivalentjuhtivus GEK vastab samaväärsele takistusele Rek = 1 / Gek.

Seejärel samaväärne ahel, mis on näidatud joonisel fig. 2, a, on joonisel fig. 2, b. Voolu vooluahela hargnemata osas koos elementide paralleelühendusega saab määrata sellest vooluringist Ohmi seaduse järgi:

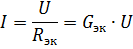
Seega, kui toitepinge on konstantne, siis paralleelselt ühendatud elementide arvu suurenemisega (mis viib samaväärse juhtivuse suurenemiseni) suureneb voolutugevus ahela hargnemata osas (toiteallika vool).

Valemist

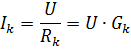
on näha, et iga haru vool sõltub ainult selle haru juhtivusest ja ei sõltu teiste harude juhtivusest. Paralleelsete harurežiimide sõltumatus üksteisest on passiivsete elementide paralleelse ühendamise oluline eelis. Tööstusseadmetes kasutatakse enamikul juhtudel elektrivastuvõtjate paralleelühendust. Kõige ilmsem näide on elektrilampide lisamine valgustusse.

Kuna paralleelühenduses rakendatakse kõigile elementidele sama pinge ja iga haru vool on võrdeline selle haru juhtivusega, on paralleelsete harude voolude suhe võrdne nende harude juhtivuste suhtega ehk pöördvõrdeline nende takistuste suhte suhtes:

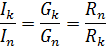
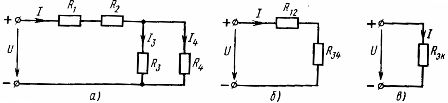
Elementide segaühendus on jada- ja paralleelühenduste kombinatsioon. Sellisel ahelal võib olla erinev arv sõlme ja harusid. Segaühenduse näide on näidatud diagrammil (joonis 3, a)

Riis. 3. Lineaarsete elementide (a) segaühenduse skeem ja sellega samaväärsed skeemid (b, c).

Sellise vooluahela arvutamiseks on vaja järjestikku määrata samaväärsed takistused nendele ahela osadele, mis on ainult jada- või ainult paralleelühendusega. Vaadeldavas vooluringis on elementide jadaühendus takistustega R1 ja R2 ning elementide paralleelühendus takistustega R3 ja R4. Kasutades eelnevalt saadud seoseid ahela elementide parameetrite vahel nende jada- ja paralleelühendusega, saab reaalset elektriahelat järjestikku asendada samaväärsete ahelatega.

Järjestikku ühendatud elementide ekvivalenttakistus

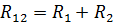
Paralleelselt ühendatud elementide R3 ja R4 ekvivalenttakistus

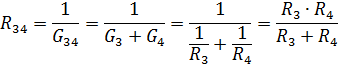
Samaväärne vooluahel elementide R12 ja R34 takistustega on näidatud joonisel fig. 3, b. Selle R12 ja R34 jadaühenduse puhul on samaväärne takistus

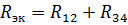
ja vastav samaväärne ahel on näidatud joonisel fig. 2, b. Leiame selle vooluahela voolu:

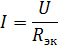
Need on toitevool ja vool reaalahela elementides R1 ja R2.Voolude I3 ja I4 arvutamiseks määrake pinge ahela takistusega R34 sektsioonis (joonis 3, b):

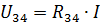
Siis saab voolud I3 ja I4 leida Ohmi seaduse järgi:

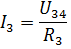
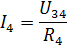
Samamoodi saate arvutada mitmeid teisi passiivsete elementide segaühendusega elektriahelaid.

Keerukate vooluahelate jaoks, millel on suur hulk ahelaid ja e. jne. c) sellist samaväärset ümberarvestamist ei saa alati läbi viia. Neid arvutatakse muude meetoditega.