Elektriahela ajakonstant - mis see on ja kus seda kasutatakse

Perioodilised protsessid on loodusele omased: päevale järgneb öö, soe aastaaeg asendub külmaga jne. Nende sündmuste periood on peaaegu konstantne ja seetõttu saab seda rangelt määrata. Veelgi enam, meil on õigus väita, et näitena toodud perioodilised looduslikud protsessid ei ole amortiseerunud, vähemalt inimese eluea osas.

Kuid tehnoloogias, eriti elektrotehnikas ja elektroonikas ei ole kõik protsessid perioodilised ja pidevad. Tavaliselt mõned elektromagnetilised protsessid esmalt suurenevad ja seejärel vähenevad. Tihti piirdub mateeria vaid võnke alguse faasiga, millel pole aega päriselt kiirust koguda.

Elektrotehnikas võib üsna sageli leida nn eksponentsiaalseid siirdeid, mille olemus seisneb selles, et süsteem lihtsalt püüab jõuda mingisse tasakaaluolekusse, mis lõpuks näeb välja nagu puhkeseisund. Selline üleminek võib olla kas suurenev või vähenev.

Välisjõud viib esmalt dünaamilise süsteemi tasakaalust välja ja seejärel ei takista selle süsteemi loomulikku naasmist algsesse olekusse. See viimane faas on nn üleminekuprotsess, mida iseloomustab teatud kestus. Lisaks on süsteemi tasakaalust välja viimise protsess ka iseloomuliku kestusega mööduv protsess.

Ühel või teisel viisil nimetatakse siirdeprotsessi ajakonstandiks selle ajakarakteristikut, mis määrab aja, mille möödudes muutub selle protsessi teatud parameeter korda «e», see tähendab, et see suureneb või väheneb umbes 2,718 korda. võrreldes algseisundiga.

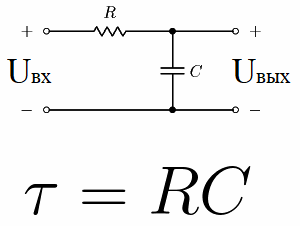
Mõelge näiteks alalispingeallikast, kondensaatorist ja takistist koosnevale elektriskeemile. Seda tüüpi vooluahelat, kus takisti on kondensaatoriga järjestikku ühendatud, nimetatakse RC-integraallülituseks.

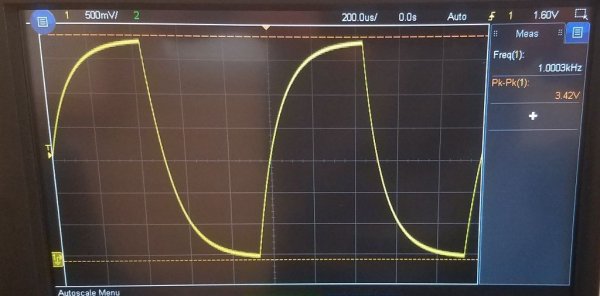
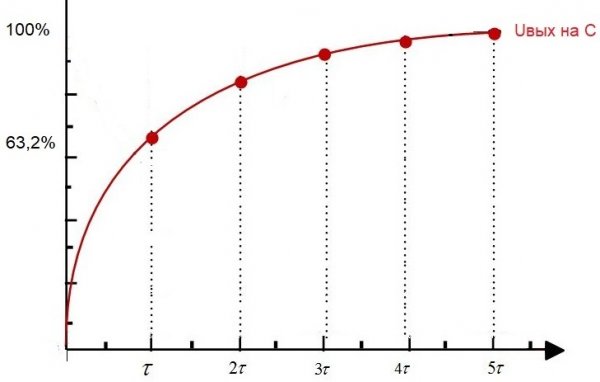
Kui sellisele vooluringile toide anda algsel hetkel, st seada sisendisse konstantne pinge Uin, siis Uout - kondensaatori pinge hakkab hüppeliselt kasvama.

Pärast aja möödumist t1 jõuab kondensaatori pinge 63,2%ni sisendpingest. Niisiis, ajavahemik alghetkest kuni t1 on selle RC-ahela ajakonstant.

Seda ahelakonstanti nimetatakse "tau", mõõdetuna sekundites ja tähistatud vastava kreeka tähega. Numbriliselt võrdub see RC-ahela puhul R * C, kus R on oomides ja C on faradides.

Integreerivaid RC-lülitusi kasutatakse elektroonikas madalpääsfiltritena, kui kõrgemad sagedused tuleb ära lõigata (alla suruda) ja madalamad sagedused läbi lasta.

Praktikas põhineb sellise filtreerimise mehhanism järgmisel põhimõttel. Vahelduvvoolu korral toimib kondensaator mahtuvusliku takistusena, mille väärtus on pöördvõrdeline sagedusega, st mida kõrgem on sagedus, seda väiksem on kondensaatori reaktants oomides.

Seega, kui vahelduvvool juhitakse läbi RC-ahela, langeb, nagu pingejaguri harul, kondensaatorile teatud pinge, mis on võrdeline selle mahtuvusega läbiva voolu sagedusel.

Kui sisend vahelduvsignaali väljalülitussagedus ja amplituud on teada, ei ole projekteerijal raske valida RC-ahelasse sellist kondensaatorit ja takistit, nii et minimaalne (lõike)pinge ( piirsagedus - sageduse ülempiir) langeb kondensaatorile, kuna reaktants siseneb jagurisse koos takistiga.

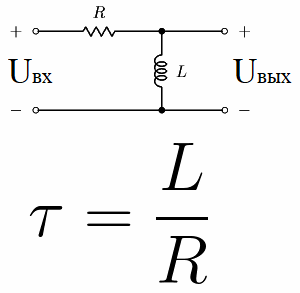
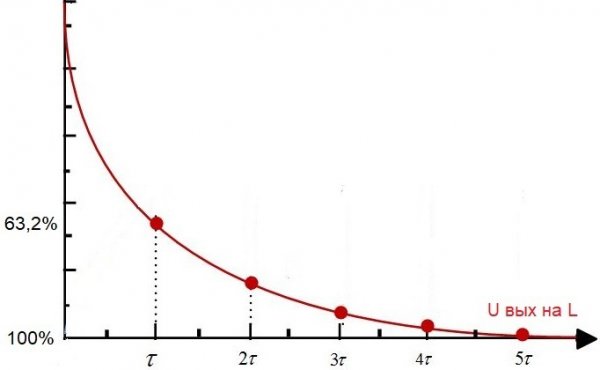
Nüüd kaaluge nn diferentseerimisahelat. See on ahel, mis koosneb järjestikku ühendatud takistist ja induktiivpoolist, RL-ahel. Selle ajakonstant on arvuliselt võrdne L / R, kus L on mähise induktiivsus henrides ja R on takisti takistus oomides.

Kui sellisele vooluringile rakendatakse allikast konstantset pinget, siis mõne aja pärast tau väheneb pooli pinge võrreldes U in-ga 63,2%, st täielikult kooskõlas selle elektriahela ajakonstandi väärtusega. .

Vahelduvvooluahelates (vahelduvad signaalid) kasutatakse LR-ahelaid kõrgpääsfiltritena, kui madalad sagedused tuleb ära lõigata (summutada) ja kõrgemad sagedused (üle piirsageduse - sageduse alumine piir) jäetakse välja.Seega, mida suurem on pooli induktiivsus, seda kõrgem on sagedus.

Nagu eespool käsitletud RC-ahela puhul, kasutatakse ka siin pingejaguri põhimõtet. Kõrgema sagedusega vool, mis läbib RL-i ahelat, põhjustab suurema pingelanguse induktiivsusel L, nagu ka induktiivtakistusega, mis on osa pingejaoturist koos takistiga. Projekteerija ülesanne on valida sellised R ja L nii, et pooli minimaalne (piir)pinge saadakse täpselt piirsagedusel.