Potentsiomeetri ja liitšundi arvutamine

Mõisted ja valemid

Potentsiomeeter on muutuv takistus liuguriga, mis on kaasas nagu näidatud joonisel fig.

Täpsemalt vaata — Potentsiomeetrid ja nende rakendused

Punktidesse 1 ja 2 rakendatakse pinge U. Punktidest 2 ja 3 eemaldatakse reguleeritav pinge, mille väärtus on väiksem kui U ja sõltub liuguri asendist. Pingejaoturitel on sarnane skeem, kuid need ei ole reguleeritavad ja neil pole liigutatavat liugurit.

Potentsiomeetrid, pingejagurid ja komplekssed šundid arvutatakse kasutades Kirchhoffi seadused, näiteks tavaliste takistustega ahelate arvutamine.

Näited

1. Lähtepinge on U = 24 V, potentsiomeetri kogutakistus r = 300 Ohm. Mootor paigaldatakse eraldi nii, et r1 = 50 oomi. Millist pinget U1 saab punktidest 3 ja 2 eemaldada (joonis 1)?

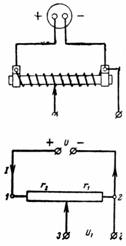
Riis. 1.

Voolu I ja pinge U takistusel r on seotud valemiga I ∙ r = U.

Potentsiomeetri liugur eraldab osa takistusest, st. takistus r1. Pingelang punktide 3 ja 2 vahel võrdub I ∙ r1 = U1.

Pingelanguse suhtest saame võrrandi (I ∙ r1) / (I ∙ r) = U1 / U. Mida suurem on takistus r1, seda suurem on pinge U1 väärtus punktide 3 ja 2 vahel U1 = r1 / r ∙ U = 50/300 ∙ 24 = 4 V.

2. Potentsiomeeter (joonis 2) on laetud lambile, mille takistus on r = 100 oomi. Potentsiomeeter jaotatakse liuguriga kaheks osaks, kus r1 = 600 oomi ja r2 = 200 oomi. Määrake pinge Ul ja lambi vool Il.

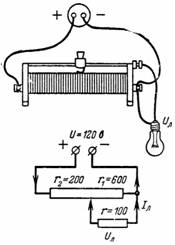
Riis. 2.

Vool I voolab läbi takistuse r2 ja vool Il läbi lambi. Läbi takistuse r1 voolab vool I-Il, mis tekitab takistuse r1 pinge, mis on võrdne lambi pingega: (I-Il) ∙ r1 = Ul.

Teisest küljest on lambi pinge võrdne lähtepingega miinus pingelangus takistusel r2: U-I ∙ r2 = Ul.

Vool I võrdub allika pingega, mis on jagatud takistuste järjestikuse paralleelühenduse takistusega:

I = U / (r2 + (r ∙ r1) / (r + r1)).

Asendame teises võrrandis allika koguvoolu avaldise:

U-U / (r2 + (r ∙ r1) / (r + r1)) ∙ r2 = Ul.

Pärast teisendust saame lambi pinge avaldise:

Ul = (U ∙ r1) / (r1 ∙ r2 + r1 ∙ r + r2 ∙ r) ∙ r.

Kui teisendame selle avaldise, alustades sellest, et Ul = Il ∙ r, siis saame lambi voolu avaldise:

Il = (U ∙ r1) / (r1 ∙ r2 + r1 ∙ r + r2 ∙ r).

Asendage saadud võrrandite arvväärtused:

Ul = (120 ∙ 600) / (600 ∙ 200 + 600 ∙ 100 + 200 ∙ 100) ∙ 100 = 7200000/200000 = 36 V;

Il = Ul / r = 36/100 = 0,36 A.

3. Arvutage potentsiomeetri osaga ühendatud mõõteseadme pinge Up ja vool Ip. Seadme takistus on r = 1000 oomi. Hargnemispunkt jagab jagaja takistuse r2 = 500 oomi ja r1 = 7000 oomi (joonis 3).Pinge potentsiomeetri klemmidel U = 220 V.

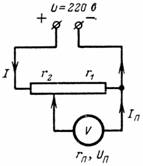
Riis. 3.

Kasutades varem saadud valemeid, võime kirjutada, et seadet läbiv vool on:

In = (U ∙ r1) / (r1 ∙ r2 + r1 ∙ r + r2 ∙ r) = (220 ∙ 7000) / (7000 ∙ 500 + 7000 ∙ 1000 + 500 ∙ 1000 + 500 ∙ 1000 + 500 ∙ 1004 = 01501) 00 = 01510 11 = 0,14 A.

Üles = Ip ∙ r = 0,14 ∙ 1000 = 14 V.

4. Arvutage seadme pinge Up, kui see tarbib voolu Ip = 20 mA ja on ühendatud potentsiomeetriga, mis on jagatud takistusteks r2 = 10 ^ 4 Ohm ja r1 = 2 ∙ 10 ^ 4 Ohm (joonis 3).

Pingejaguri kogupinge võrdub selle osade pingelanguste summaga (läbi takistuste r1 ja r2): U = I ∙ r2 + I1 ∙ r1; U = I ∙ r2 + Üles

Lähtevool on mootori kontaktpunktis hargnenud: I = I1 + Ip; I = Upn / r1 + In.

Asendame pingevõrrandis voolu I väärtuse:

U = (Un / r1 + In) ∙ r2 + Un;

U = Uп / r1 ∙ r2 + Iп ∙ r2 + Uп;

U = Upn ∙ (r2 / r1 +1) + In ∙ r2.

Seetõttu on seadme pinge Upn = (U-In ∙ r2) / (r1 + r2) ∙ r1.

Asendage arvväärtused: Üles = (220-0,02 ∙ 10000) / 30000 ∙ 20000 = 20/3 ∙ 2 = 13,3 V.

5. Alalisvooluallikas pingega U = 120 V toidab raadiovastuvõtja anoodahelaid läbi potentsiomeetri (pingejaguri), mille takistus koos filtriga on r = 10000 Ohm. Pinge U1 eemaldatakse takistusega r2 = 8000 oomi. Arvutage anoodi pinge tühikäigul ja koormusvoolul I = 0,02 A (joonis 4).

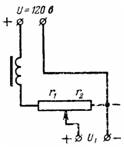
Riis. 4.

Esimene juhtum on sarnane näitega 1:

U: U1 = r: r2;

U1 = r2 / r ∙ U = 8000/10000 ∙ 120 = 96 V.

Teine juhtum on sarnane näitega 3:

U1 = (U-I ∙ r1) / r ∙ r2;

U1 = (120-0,02 ∙ 2000) / 10000 ∙ 8000 = 64 V.

Laadimisel langeb pinge 96 V-lt 64 V-le.Kui on vaja rohkem pinget, tuleks liugurit vasakule liigutada, st suurendada takistust r2.

6. Pinged Ua ja Ub eemaldatakse pingejaguriga. Pingega U1 = 220 V ühendatud pingejaguri kogutakistus on r = 20 000 Ohm. Kui suur on pinge Ua takistuses r3 = 12000 oomi voolutarbimisega Ia = 0,01 A ja pinge Ub takistuses r2 + r3 = 18000 oomi voolutarbimisega Ib = 0,02 A (joonis 5).

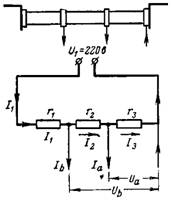
Riis. 5.

Pingetakistus r3

Ua = I3 ∙ r3;

Ua = (U -Ia ∙ (r1 + r2) -Ib ∙ r1) / r ∙ r3;

Ua = (220-0,01 ∙ 8000-0,02 ∙ 2000) / 20 000 ∙ 12 000 = (220-80-40) / 20 ∙ 12 = 60 V.

Pinge Ub võrdub takistuse r3 pingelangu Ua ja takistuse r2 pingelanguse summaga. Pingelangus takistuse r2 juures on võrdne I2 ∙ r2. Praegune I2 = Ia + I3. Voolu I3 saab arvutada nagu näites 1:

I3 = (220-80-40) / 20 000 = 0,005 A;

I2 = Ia + I3 = 0,01 + 0,005 = 0,015 A.

Pinge Ub = Ua + I2 ∙ r2 = 5 + 0,015 ∙ 6000 = 150 V.

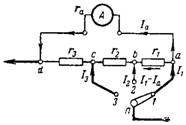
7. Arvutage milliampermeetri kombineeritud šunt nii, et lüliti erinevates asendites oleks sellel järgmised mõõtevahemikud: I1 = 10 mA; I2 = 30 mA; I3 = 100mA. Šundi ühendusskeem on näidatud joonisel fig. 6. Seadme sisetakistus ra = 40 Ohm. Sisemine mõõtevahemik milliampermeeter 2 mA.

Riis. 6.

Voolu I≤2mA mõõtmisel lülitatakse šunt välja.

a) Voolu I = 10 mA mõõtmisel on lüliti asendis 1 ja läbi kõigi šunditakistuste voolab vool 10-2 = 8 mA. Pingelang šundi takistuse Ush ja seadme Ua vahel punktide d ja a vahel peab olema sama

Ush = Ua;

(I1-Ia) ∙ (r1 + r2 + r3) = Ia ∙ ra;

0,008 ∙ (r1 + r2 + r3) = 0,002 ∙ 40.

b) Voolu I2 = 30 mA mõõtmisel on lüliti asendis 2. Mõõdetud vool jaguneb punktis b. Seadme osuti täieliku kõrvalekalde korral läbib takistust r1 ja seadet ra vool Ia = 2 mA.

Ülejäänud vool I2-Ia läbib takistusi r2 ja r3. Voolud tekitavad sama pingelanguse kahe haru vahel punktide d ja b vahel:

(I2-Ia) ∙ (r2 + r3) = Ia ∙ r1 + Ia ∙ ra;

(0,03-0,002) ∙ (r2 + r3) = 0,002 ∙ (r1 + 40).

c) Sarnaselt teostame arvutuse mõõtmisvahemiku suurendamisel I3 = 100 mA-ni. Vool I3-Ia voolab läbi takistuse r3 ja vool Ia läbi takistuste r1, r2, ra. Mõlema haru pinge on sama: (I3-Ia) ∙ r3 = Ia ∙ r1 + Ia ∙ r2 + Ia ∙ ra;

0,098 ∙ r3 = 0,002 ∙ (r1 + r2 + 40).

Saime kolm võrrandit kolme tundmatu takistuse väärtusega r1, r2 ja r3.

Korrutame kõik võrrandid 1000-ga ja teisendame need:

r1 + r2 + r3 = 10;

14 ∙ (r2 + r3) -r1 = 40;

49 ∙ r3-r1-r2 = 40.

Liidame kokku esimese ja kolmanda võrrandi: 50 ∙ r3 = 50;

r3 = 50/50 = 1 ohm.

Liidame kokku esimese ja teise võrrandi: 15 ∙ r2 + 15 ∙ r3 = 50;

15 ∙ r2 + 15 ∙ 1 = 50;

15 ∙ r2 = 35; r2 = 2,34 oomi.

Asendame saadud tulemused esimeses võrrandis: r1 + 35/15 + 1 = 10;

15 ∙ r1 + 35 + 15 = 150;

r1 = 100/15 = 6,66 oomi.

Arvutuse õigsust saab kontrollida, asendades saadud takistuse väärtused võrranditesse.