Saadud takistuse arvutamine jada-paralleelühenduses
Mõisted ja valemid
Jada-paralleel- või segaühendus on kolme või enama takistuse kompleksühendus. Segaühenduse tekkiv takistus arvutatakse etapiviisiliselt, kasutades seeria- ja paralleelühenduste takistuste arvutamise valemeid.
Näited
1. Arvutage kolme takistuse jada-paralleelühendus vastavalt joonisel fig. 1.
Esmalt asendage paralleelselt ühendatud takistused r2 ja r3 saadud takistusega r (2-3):
r (2-3) = (r2 ∙ r3) / (r2 + r3) = (10 ∙ 20) / 30 = 6,6 oomi.
Saadud kogu vooluahela takistus on r = r1 + r (2-3) = 5 + 6,6 = 11,6 oomi.
Riis. 1.
2. Milline vool läbib ahelat (joonis 2) avatud ja suletud juhtudel noa lüliti P? Kuidas muutub pinge takistuse r2 mõlemal juhul?
Riis. 2.
a) Lüliti on avatud. Järjestikku ühendatud takistuste r1 ja r2 tulenev takistus
r (1-2) = r1 + r2 = 25 oomi.
Vool I (1-2) = U / r (1-2) = 100/25 = 4 A.
Pingelangus üle takistuse r2
U2 = I (1-2) ∙ r2 = 4 ∙ 5 = 20 V.
b) Lüliti on suletud. Paralleelselt ühendatud takistite r1 ja r3 tulenev takistus
r (1-3) = (r1 ∙ r3) / (r1 + r3) = (20 ∙ 10) / (20 + 10) = 200/30 = 6,6 oomi.
Kogu vooluahela kogutakistus on r = r (1-3) + r2 = 6,6 + 5 = 11,6 oomi.
Vool I = U / r = 100 / 11,6 = 8,62 A.
Pingelangus takistusel r2 on sel juhul võrdne: U2 = I ∙ r2 = 8,62 ∙ 5 = 43,25 V.
Teisel juhul suurenes vool paralleeltakistuse R3 ühendamise tulemusena. Rohkem voolu loob rohkem pingelangus takistusel r2.
3. Mis peaks olema täiendav vastupanu rd, et kaks paralleelselt ühendatud lampi pingele 120 V ja voolule 0,2 A saaks ühendada U = 220 V pingega võrku (joonis 3)?
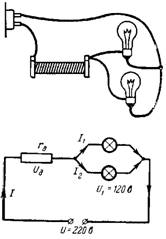
Riis. 3.
Lampide pinge peaks olema võrdne 120 V. Ülejäänud pinge (100 V) langeb lisatakistusele rd. Läbi takistuse rd voolab kahe lambi vool I = 0,4 A.
Ohmi seaduse kohaselt rd = Ud / I = 100 / 0,4 = 250 Ohm.
4. Elektroonilised lambid 1,2 V hõõgniidi ja hõõgniidi vooluga 0,025 ja 0,05 A on ühendatud järjestikku alalisvoolu allikaga pinge 4,5 V. Milline peaks olema lisatakistus rd ja paralleeltakistus (šunt) väiksema hõõgniidivooluga lambile (joonis 4)?
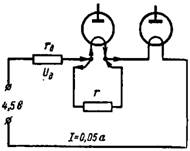
Riis. 4.
Ahela takistused tuleb valida nii, et teise lambi hõõgniidi vool voolaks I = 0,05 A. Elektrooniliste lampide hõõgniidi pinge on 1,2 + 1,2 = 2,4 V. Lahutades selle väärtuse aku pingest, saame võtke lisatakistuse rd pingelanguse väärtus: Ud = 4,5-2,4 = 2,1 V.
Seetõttu lisatakistus rd = (Ud) / I = 2,1 / 0,05 = 42 oomi.
Hõõgniidi vool 0,05 A ei tohiks läbida esimese vaakumtoru hõõgniidi. Pool sellest voolust (0,05-0,025 = 0,025 A) peab läbima šundi r. Šundi pinge on sama, mis lambi hõõgniidil, st. 1,2 V. Seetõttu on šundi takistus: r = 1,2 / 0,025 = 48 Ohm.
5. Mis on saadud vooluahela takistus ja vool selles joonisel fig. 5?
Riis. 5.
Esiteks määrame paralleelselt ühendatud takistite takistuse:
r (1-2) = (r1 ∙ r2) / (r1 + r2) = (2 ∙ 4) / (2 + 4) = 8/6 = 1,3 oomi;
r (4-5) = (r4 ∙ r5) / (r4 + r5) = (15 ∙ 5) / (15 + 5) = 75/20 = 3,75 oomi.
Saadud vooluahela takistus on:
r = r (1-2) + r3 + r (4-5) = 1,3 + 10 + 3,75 = 15,05 oomi.
Saadud vool pingel U = 90,5 V
I = U / r = 90,5 / 15,05 = 6 A.
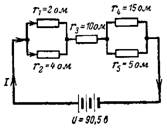
6. Arvutage kompleksse jada-paralleelühenduse takistus joonisel fig. 6. Arvutage saadud vool I, vool I4 ja pingelang takistusel r1.
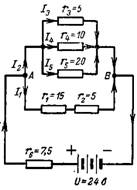
Riis. 6.
Paralleelselt ühendatud takistuste juhtivus
1 / r (3-4-5) = 1 / r3 + 1 / r4 + 1 / r5 = 1/5 + 1/10 + 1/20 = 7/20 sim;
r (3-4-5) = 20/7 = 2,85 oomi.
R1 ja r2 vooluahela takistus on:
r (1-2) = r1 + r2 = 15 + 5 = 20 oomi.
Saadud juhtivus ja takistus punktide A ja B vahel on vastavalt võrdsed: 1 / rAB = 1 / r (3-4-5) + 1 / r (1-2) = 7/20 + 1/20 = 8/20 sim ; rAB = 20/8 = 2,5 oomi.
Saadud kogu vooluahela takistus on r = rAB + r6 = 2,5 + 7,5 = 10 oomi.
Saadud vool on I = U / r = 24/10 = 2,4 A.
Punktide A ja B vaheline pinge on võrdne lähtepingega U miinus pingelang takistil r6
UAB = U-I ∙ r6 = 24-(2,4 ∙ 7,5) = 6V.
Selle pingega on ühendatud takistus r4, nii et seda läbiv vool on võrdne:
I4 = UAB / r4 = 6/10 = 0,6A.
Takistitel r1 ja r2 on ühine pingelang UAB, seega vool läbi r1 on:
I1 = UAB / r (1-2) = 6/20 = 0,3 A.
Pingelangus üle takistuse r1
Ur1 = I1 ∙ r1 = 0,3 ∙ 15 = 4,5 V.
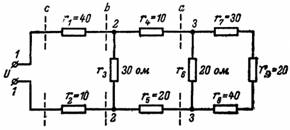
7. Milline on saadud takistus ja vool joonisel fig. 7 kui lähtepinge on U = 220 V?
Riis. 7.
Alustame ahelast, mis asub sõlmedest 3 ja 3 paremal. Takistid r7, r8, r9 on ühendatud järjestikku, seega
r (7-8-9) = r7 + r8 + r9 = 30 + 40 + 20 = 90 oomi.
Selle takistusega paralleelselt on ühendatud takistus r6, nii et saadud takistus sõlmedes 3 ja 3 (jaotis a)
ra = (r6 ∙ r (7-8-9)) / (r6 + r (7-8-9)) = (20 ∙ 90) / (20 + 90) = 1800/110 = 16,36 oomi.
Takistid r4 ja r5 on ühendatud takistusega ra järjestikku:
r (4-5-a) = 10 + 20 + 16,36 = 46,36 oomi.
Sõlmede 2 ja 2 tulenev takistus (jaotis b)
rb = (r (4-5-a) ∙ r3) / (r (4-5-a) + r3) = (46,36 ∙ 30) / (46,36 + 30) = 1390,8 / 76, 36 = 18,28 oomi.
Saadud kogu vooluahela takistus on r = r1 + rb + r2 = 40 + 18,28 + 10 = 68,28 oomi.
Saadud vool on I = U / r = 220 / 68,28 = 3,8 A.