Impulssvool

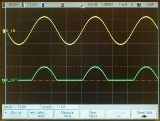Erinevates elektroonikaseadmetes, näiteks elektroonika- ja pooljuhtseadmetes, st võimendites, alaldites, raadiotes, generaatorites, televiisorites, aga ka süsinikmikrofonides, telegraafides ja paljudes teistes seadmetes kasutatakse neid laialdaselt pulsatsioonivoolude ja pingete ... mitte korrata arutluskäiku kaks korda, räägime ainult vooludest, kuid kõik, mis on seotud vooludega, kehtib ka pingete kohta.

Pulseerivad voolud, millel on konstantne suund, kuid muudavad nende väärtust, võivad olla erinevad. Mõnikord muutub praegune väärtus kõrgeimast madalaimaks nullist erinevaks väärtuseks. Muudel juhtudel vähendatakse voolu nullini. Kui alalisvoolu ahel on teatud sagedusel katkenud, siis teatud ajavahemike jooksul vooluringis ei ole.

Joonisel fig. 1 näitab erinevate lainevoolude graafikuid. Joonisel fig. 1, a, b, voolude muutus toimub vastavalt sinusoidne kõver, kuid neid voolusid ei tohiks pidada siinusekujulisteks vahelduvvooludeks, kuna voolu suund (märk) ei muutu. Joonisel fig.1, c näitab voolu, mis koosneb eraldi impulssidest, st lühiajalistest voolu "löökidest", mis on üksteisest eraldatud pikema või väiksema kestusega pausidega ja mida sageli nimetatakse impulssvooluks. Erinevad impulssvoolud erinevad üksteisest nii impulsside kuju ja kestuse kui ka kordussageduse poolest.

Igasugust pulseerivat voolu on mugav käsitleda kahe voolu – alalis- ja vahelduvvoolu – summana, mida nimetatakse termini- või komponentvooludeks. Igal pulseerival voolul on alalis- ja vahelduvvoolukomponendid. See tundub paljudele kummaline. Tegelikult on pulseeriv vool ju vool, mis voolab kogu aeg ühes suunas ja muudab selle väärtust.

Kuidas aru saada, et see sisaldab suunda muutvat vahelduvvoolu? Kui aga kaks voolu — otsene ja vahelduv — läbivad samaaegselt sama juhtme, siis selgub, et selles juhtmes liigub pulseeriv vool (joonis 2). Sel juhul ei tohiks vahelduvvoolu amplituud ületada alalisvoolu väärtust. Alalis- ja vahelduvvool ei saa traadist eraldi voolata. Need lisavad üldisele elektronide voolule, millel on kõik pulseeriva voolu omadused.

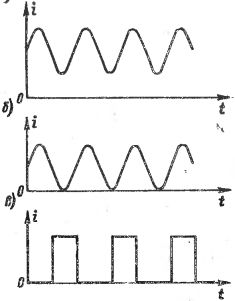
Riis. 1. Erinevate lainevoolude graafikud

Vahelduv- ja alalisvoolude liitmist saab näidata graafiliselt. Joonisel fig. 2 on kujutatud alalisvoolu 15 mA ja vahelduvvoolu amplituudiga 10 mA graafikuid. Kui liidame nende voolude väärtused üksikute ajahetkede kohta, võttes arvesse voolude suundi (märke), saame joonisel fig 1 näidatud lainevoolu graafiku. 2 paksu joonega. See vool varieerub madalaimast 5 mA-st kuni 25 mA-ni.

Kaalutud voolude liitmine kinnitab pulseeriva voolu esituse paikapidavust alalis- ja vahelduvvoolude summana. Selle esituse õigsust kinnitab ka asjaolu, et mõne seadme abil on võimalik selle voolu komponente üksteisest eraldada.

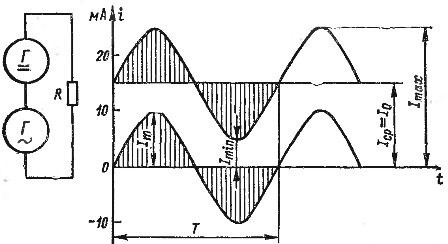
Riis. 2. Pulseeriva voolu saamine alalis- ja vahelduvvoolu lisamise teel.

Tuleb rõhutada, et iga voolu saab alati esitada mitme voolu summana. Näiteks voolutugevust 5 A võib pidada ühes suunas voolavate voolude 2 ja 3 A summaks või eri suundades voolavate voolude 8 ja 3 A summaks ehk teisisõnu voolude 8 erinevuseks. ja 3 A. Pole raske leida muid kahe või enama voolu kombinatsioone, mis annavad kokku 5 A.

Siin on täielik sarnasus jõudude liitmise ja lagunemise põhimõttega. Kui mis tahes objektile mõjuvad kaks võrdselt suunatud jõudu, saab need asendada ühe ühise jõuga. Vastassuunas mõjuvaid jõude saab asendada ühikulise erinevusega. Ja vastupidi, antud jõudu võib alati pidada vastavate võrdselt suunatud jõudude summaks või vastassuunaliste jõudude vaheks.

Alalis- või sinusoidaalseid vahelduvvoolusid ei ole vaja lagundada komponentvooludeks. Kui asendada pulseeriv vool alalis- ja vahelduvvoolu summaga, siis rakendades nendele komponentvooludele teadaolevaid alalis- ja vahelduvvoolu seadusi, on võimalik lahendada paljusid pulseeriva vooluga seotud probleeme ja teha vajalikke arvutusi.

Pulseeriva voolu mõiste alalis- ja vahelduvvoolu summana on tavapärane.Muidugi ei saa eeldada, et teatud ajavahemike järel voolavad otse- ja vahelduvvoolud tõesti mööda traati üksteise poole. Tegelikult pole kahte vastandlikku elektronide voogu.

Tegelikult on pulseeriv vool üksikvool, mis muudab aja jooksul oma väärtust. Õigem on öelda, et pulseerivat pinget või pulseerivat EMF-i saab esitada konstantse ja muutuva komponendi summana.

Näiteks joonisel fig. 2 näitab, kuidas algebraliselt liidetakse ühe generaatori konstant emf teise generaatori muutujale emf. Selle tulemusena on meil pulseeriv EMF, mis põhjustab vastava pulseeriva voolu. Tinglikult võib aga arvestada, et konstantne EMF tekitab ahelas alalisvoolu ja vahelduv EMF - vahelduvvool, mis summeerides moodustab pulseeriva voolu.

Iga pulseerivat voolu saab iseloomustada Itaxi ja Itini maksimaalse ja minimaalse väärtusega, samuti selle konstantsete ja muutuvate komponentidega. Konstantset komponenti tähistatakse I0-ga. Kui vahelduvkomponent on siinusvool, siis selle amplituudi tähistatakse Itiga (kõik need suurused on näidatud joonisel 2).

Seda ei tohiks segi ajada It ja Itaxiga. Samuti ei tohiks voolulaine Imax maksimaalset väärtust nimetada amplituudiks. Mõiste amplituud viitab tavaliselt ainult vahelduvvooludele. Pulseeriva voolu puhul saame rääkida ainult selle muutuva komponendi amplituudist.

Pulseeriva voolu konstantset komponenti võib nimetada selle keskmiseks väärtuseks Iav, see tähendab aritmeetiliseks keskmiseks väärtuseks. Tõepoolest, kui arvestada joonisel fig 1 näidatud pulseeriva voolu ühe perioodi muutusi.2, on selgelt näha: esimesel poolperioodil lisatakse 15 mA voolule hulk väärtusi, muutes voolukomponenti, varieerudes vahemikus 0 kuni 10 mA ja tagasi 0-ni ning teisel poolel -tsükkel, voolust 15 mA lahutatakse täpselt samad vooluväärtused.

Seetõttu on vool 15 mA tõesti keskmine väärtus. Kuna vool on elektrilaengute ülekanne läbi juhtme ristlõike, siis Iav on sellise alalisvoolu väärtus, mis ühel perioodil (või terve arvu perioodide jooksul) kannab sama palju elektrit kui see pulseeriv vool .

Sinusoidse vahelduvvoolu korral on Iav väärtus perioodi kohta null, kuna ühel poolperioodil juhi ristlõike läbinud elektrienergia hulk on võrdne teisel poolperioodil vastupidises suunas läbinud elektrienergia kogusega. Voolugraafikute graafikutel, mis näitavad voolu i sõltuvust ajast t, väljendatakse vooluga kantud elektri kogust voolukõveraga piiratud joonise pindalaga, kuna elektrienergia koguse määrab toode, mida see .

Sinusoidse voolu korral on positiivse ja negatiivse poollainete pindalad võrdsed.Joonis fig. 2, esimese poolperioodi jooksul liidetakse vahelduvvoolu komponendi poolt kantud elektrienergia kogus voolu Iav poolt kantud elektrikogusele (joonisel varjutatud ala). Ja teise pooltsükli jooksul eemaldatakse täpselt sama palju elektrit. Selle tulemusena kantakse kogu perioodi jooksul üle sama kogus elektrit kui ühe alalisvoolu Iav korral, see tähendab, et ristküliku Iav T pindala on võrdne lainevoolu kõveraga piiratud pindalaga.

Seega määratakse voolu konstantne komponent ehk keskmine väärtus elektrilaengute ülekandmisega läbi juhtme ristlõike.

Praegune võrrand, mis on näidatud joonisel fig. 2 tuleks ilmselt kirjutada järgmisel kujul:

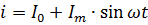
Pulseeriva voolu võimsus tuleb arvutada selle komponentvoolude võimsuste summana. Näiteks kui joonisel fig. 2, läbib takistusega R takisti, siis selle võimsus on

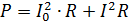
kus I = 0,7Im on muutuva komponendi efektiivväärtus.

Saate tutvustada lainevoolu Id efektiivväärtuse mõistet. Võimsus arvutatakse tavalisel viisil:

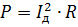
Võrdsustades selle avaldise eelmisega ja taandades selle R-ga, saame:

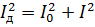
Samasuguseid seoseid võib saada ka pingete puhul.