Mis on sisemine takistus

Oletame, et on olemas lihtne elektriline suletud vooluahel, mis sisaldab vooluallikat, näiteks generaatorit, galvaanielementi või akut ja takistust R. Kuna voolutugevus ahelas ei katke kuskil, siis voolab see ka allika sees.

Sellises olukorras võime öelda, et igal allikal on mingi sisemine takistus, mis takistab voolu liikumist. See sisemine takistus iseloomustab vooluallikat ja seda tähistatakse tähega r. Sest galvaaniline element või aku, sisetakistus on elektrolüüdi lahuse ja elektroodide takistus, generaatori puhul - staatori mähiste takistus jne.

Seega iseloomustab vooluallikat nii EMF-i suurus kui ka tema enda sisetakistuse r väärtus — mõlemad omadused näitavad allika kvaliteeti.

Kõrgepinge elektrostaatilised generaatorid (nagu Van de Graafi generaator või Wimshursti generaator) omavad näiteks tohutut EMF-i, mida mõõdetakse miljonites voltides, samas kui nende sisetakistust mõõdetakse sadades megaoomides, mistõttu need ei sobi suured voolud.

Vastupidi, galvaaniliste elementide (näiteks aku) EMF on suurusjärgus 1 volt, kuigi nende sisetakistus on murdosa või kõige rohkem kümme oomi suurust ning seetõttu on võimalik saada ühikute ja kümnete amprite suurust voolu galvaanilistest elementidest.

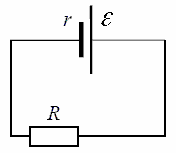
See diagramm näitab tegelikku allikat ühendatud koormusega. Need on siin määratletud EMF allikas, selle sisetakistus ja ka koormustakistus. Vastavalt Ohmi seadus suletud ahela jaoks, on selle ahela vool võrdne:

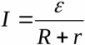
Kuna välisahela osa on homogeenne, saab Ohmi seadusest leida koormuse pinge:

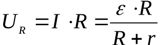
Väljendades koormuse takistust esimesest võrrandist ja asendades selle väärtuse teise võrrandiga, saame koormuse pinge sõltuvuse voolust suletud ahelas:

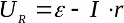
Suletud ahelas on EMF võrdne väliste vooluahela elementide ja allika enda sisemise takistuse pingelanguse summaga. Koormuspinge sõltuvus koormusvoolust on ideaalis lineaarne.

Graafik näitab seda, kuid tegeliku takisti katseandmed (ristid graafiku lähedal) erinevad alati ideaalist:

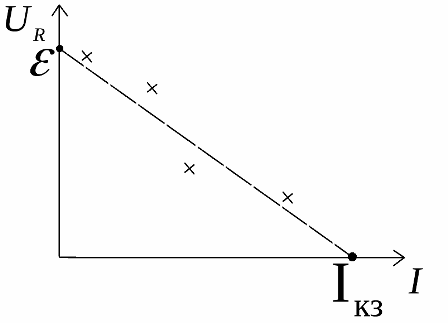
Katsed ja loogika näitavad, et nullkoormuse voolu korral on välise vooluahela pinge võrdne allika emf-ga ja nullkoormuse pinge korral on vooluahela vool lühise vool… See reaalahelate omadus aitab eksperimentaalselt leida tõeliste allikate EMF-i ja sisetakistust.

Sisemise takistuse eksperimentaalne tuvastamine

Nende omaduste eksperimentaalseks määramiseks koostatakse koormuse pinge sõltuvuse graafik voolu suurusest, mille järel ekstrapoleeritakse see telgede lõikepunkti.

Graafiku lõikepunktis pinge selgrooga on allika emf väärtus ja voolu teljega lõikepunktis lühisvoolu väärtus. Selle tulemusena leitakse sisemine takistus järgmise valemi abil:

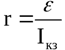
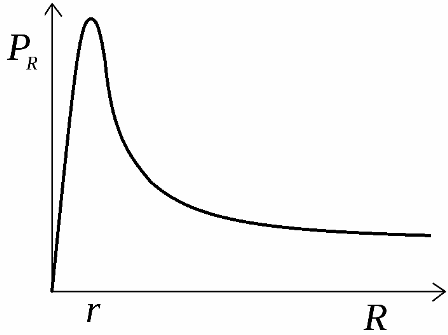
Allika poolt välja töötatud kasulik võimsus jaotatakse üle koormuse. Selle võimsuse sõltuvuse graafik koormustakistusest on näidatud joonisel. See kõver algab koordinaattelgede lõikepunktist nullpunktis, seejärel tõuseb maksimaalse võimsuse väärtuseni, seejärel langeb nullini, kui koormustakistus on võrdne lõpmatusega.

Maksimaalse koormustakistuse leidmiseks, mille juures teoreetiline maksimaalne võimsus antud allikaga arendatakse, võetakse võimsusvalemi tuletis R suhtes ja see nullitakse. Maksimaalne võimsus areneb siis, kui välisahela takistus on võrdne sisemise allika takistusega:

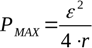
See maksimaalse võimsuse säte R = r korral võimaldab teil eksperimentaalselt leida allika sisetakistuse, joonistades koormusel vabaneva võimsuse ja koormuse takistuse väärtuse.Maksimaalset võimsust tagava tegeliku, mitte teoreetilise koormustakistuse leidmine määrab toiteallika tegeliku sisemise takistuse.

Vooluallika kasutegur näitab koormusele jaotatud maksimaalse võimsuse ja hetkel arendatava koguvõimsuse suhet

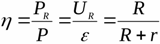
On selge, et kui allikas arendab sellist võimsust, et koormuse juures saadakse antud allika jaoks maksimaalne võimalik võimsus, siis on allika kasutegur 50%.