Pingete, takistuste ja võimsuste kolmnurgad
Kõik, kellel on vektorskeemidest aimu, märkavad kergesti, et neil on väga selgelt eristatav täisnurkne pingekolmnurk, mille iga külg peegeldab: vooluahela kogupinget, aktiivtakistuse pinget ja pinget. reaktsioonivõime kohta.
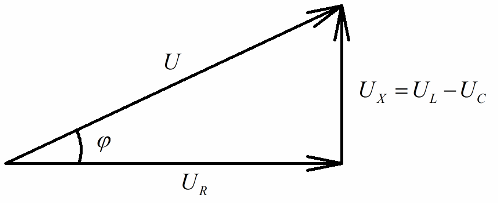
Vastavalt Pythagorase teoreemile näeb nende pingete (ahela kogupinge ja selle sektsioonide pinge vahel) suhe välja järgmine:
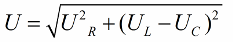
Kui järgmiseks sammuks on nende pingete väärtuste jagamine vooluga (vool läbib jadaahela kõiki sektsioone võrdselt), siis Ohmi seadus saame takistuse väärtused, see tähendab, et nüüd saame rääkida täisnurksest takistuste kolmnurgast:
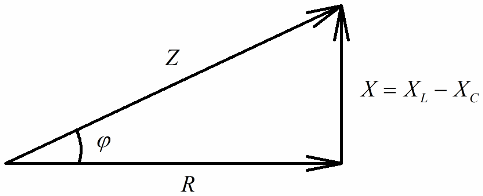
Sarnasel viisil (nagu pingete puhul) on Pythagorase teoreemi kasutades võimalik luua seos ahela impedantsi ja reaktantsuste vahel. Seost väljendatakse järgmise valemiga:
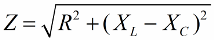
Seejärel korrutame takistuse väärtused vooluga, tegelikult suurendame täisnurkse kolmnurga mõlemat külge teatud arv kordi. Selle tulemusena saame täisnurkse kolmnurga võimsustega:
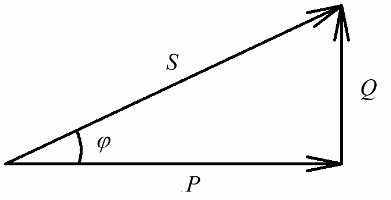
Aktiivvõimsus, mis vabaneb vooluahela aktiivtakistusest, mis on seotud elektrienergia pöördumatu muundamisega (soojuseks, paigaldises töö tegemisel), on selgelt seotud reaktiivvõimsusega, mis on seotud energia pöörduva muundamisega (loomine). magnet- ja elektriväljad mähistes ja kondensaatorites) ning elektripaigaldise täisvõimsusega.
Aktiivvõimsust mõõdetakse vattides (W), reaktiivvõimsust — variides (VAR — volt-amper reaktiiv), kogu — VA-des (volt-amper).
Pythagorase teoreemi kohaselt on meil õigus kirjutada:
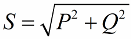
Pöörame nüüd tähelepanu sellele, et võimsuskolmnurgas on nurk phi, mille koosinust on lihtne määrata eelkõige aktiivvõimsuse ja näivvõimsuse järgi. Selle nurga koosinus (cos phi) nimetatakse võimsusteguriks. See näitab, kui suur osa koguvõimsusest läheb elektripaigaldises kasuliku töö tegemisel arvele ja seda ei tagastata võrku.
Ilmselgelt näitab kõrgem võimsustegur (maksimaalselt üks) jaama tööks tarnitud energia suuremat muundamise efektiivsust. Kui võimsustegur on 1, siis kogu tarnitud energia kasutatakse töö tegemiseks.
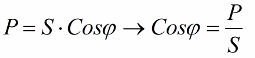
Saadud suhted võimaldavad väljendada paigaldise voolutarbimist võimsusteguri, aktiivvõimsuse ja võrgupinge kaudu:
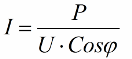
Seega, mida väiksem on koosinus phi, seda rohkem voolu vajab võrk teatud töö tegemiseks. Praktikas piirab see tegur (maksimaalne võrguvool) ülekandeliini ülekandevõimsust ja seetõttu, mida madalam on võimsustegur, seda suurem on liini koormus ja väiksem kasulik ribalaius (madal koosinus phi põhjustab piiranguid). Kahaneva koosinusphiga elektriliinide džaulikadusid saab näha järgmisest valemist:
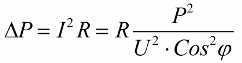
Ülekandeliini aktiivsel takistusel R kaod suurenevad, mida suurem on vool I, kuigi see reageerib koormusele. Seetõttu võime öelda, et väikese võimsusteguriga elektri edastamise maksumus lihtsalt tõuseb. See tähendab, et koosinuse phi suurendamine on oluline rahvamajanduslik ülesanne.
Soovitav on, et koguvõimsuse reaktiivkomponent läheneks nullile.Selleks oleks hea kasutada elektrimootoreid ja trafosid alati täiskoormusel ning need kasutuse lõpus välja lülitada, et tühikäigul ei käiks. Koormatuseta on mootoritel ja trafodel väga madal võimsustegur. Üks viis koosinus phi suurendamiseks kasutajate hulgas on kasutada kondensaatoripangad ja sünkroonsed kompensaatorid.
