Aktiivne takistus ja induktiivpool vahelduvvooluahelas

Arvestades ainult induktiivset takistust sisaldavat vahelduvvooluahelat (vt artiklit "Induktor vahelduvvooluahelas"), eeldasime, et selle vooluahela aktiivne takistus on null.

Tegelikult on nii mähise enda traat kui ka ühendusjuhtmed väikese, kuid aktiivse takistusega, mistõttu vooluahel kulutab paratamatult vooluallika energiat.

Seetõttu on välise vooluahela kogutakistuse määramisel vaja lisada selle reaktiiv- ja aktiivtakistus. Kuid on võimatu lisada neid kahte erinevat laadi takistust.

Sel juhul leitakse ahela takistus vahelduvvoolule geomeetrilise liitmise teel.

Ehitatakse täisnurkne kolmnurk (vt joonis 1), mille üks pool on induktiivtakistuse väärtus ja teine ​​pool aktiivtakistuse väärtus. Soovitud voolutakistus määratakse kolmnurga kolmanda külje järgi.

Joonis 1. Induktiiv- ja aktiivtakistust sisaldava vooluahela impedantsi määramine

Vooluahela takistust tähistatakse ladina tähega Z ja seda mõõdetakse oomides. Konstruktsioonist on näha, et kogutakistus on alati suurem kui induktiivne ja aktiivtakistus eraldi võetuna.

Kogu vooluahela takistuse algebraline avaldis on:

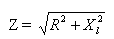
kus Z — kogutakistus, R — aktiivtakistus, XL — ahela induktiivne takistus.

Seetõttu on vooluahela kogutakistus vahelduvvoolule, mis koosneb aktiivsest ja induktiivsest takistusest, võrdne selle vooluahela aktiivse ja induktiivse takistuse ruutude summa ruutjuurega.

Ohmi seadus kuna sellist vooluringi väljendatakse valemiga I = U / Z, kus Z on ahela kogutakistus.

Analüüsime nüüd, milline saab olema pinge, kui vooluahelal on lisaks ja ja faasinihkele voolu ja induktiivsuse vahel ka suhteliselt suur aktiivtakistus. Praktikas võib selliseks vooluringiks olla näiteks ahel, mis sisaldab peenikese juhtmega (kõrgsageduslik drossel) keeratud raudsüdamiku induktiivpooli.

Sel juhul ei ole faasinihe voolu ja pinge vahel enam veerand perioodi (nagu see oli ainult induktiivse takistusega vooluringis), vaid palju väiksem; ja mida suurem on takistus, seda väiksem on faasinihe.

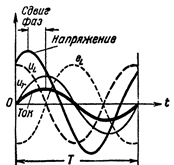
Joonis 2. Vool ja pinge ahelas, mis sisaldab R ja L.

Nüüd ta ise Eneseinduktsiooni EMF ei ole vooluallika pingega antifaasis, kuna see on pinge suhtes nihkes mitte poole perioodi võrra, vaid vähem.Lisaks ei ole pooli klemmides vooluallika tekitatud pinge võrdne iseinduktsiooni emf-ga, vaid on sellest suurem pooli juhtme aktiivtakistuse pingelanguse võrra. Teisisõnu koosneb mähises olev pinge niikuinii kahest komponendist:

• tiL- pinge reaktiivne komponent, mis tasakaalustab iseinduktsioonist tuleneva EMF-i mõju,

• tiR- pinge aktiivne komponent, mis ületab vooluahela aktiivse takistuse.

Kui ühendada mähisega järjestikku suur aktiivtakistus, väheneb faasinihe nii palju, et voolu siinuslaine jõuab peaaegu pinge siinuslainele järele ja faaside erinevus nende vahel on vaevumärgatav. liikme amplituud ja on suurem kui termini amplituud.

Samamoodi saate faasinihet vähendada ja isegi täielikult nulli viia, kui generaatori sagedust mingil viisil vähendate. Sageduse vähenemine toob kaasa iseinduktsiooni EMF vähenemise ja seega ka sellest põhjustatud voolu ja pinge vahelise faasinihke vähenemise.

Induktiivpooli sisaldava vahelduvvooluahela võimsus

Pooli sisaldav vahelduvvooluahel ei tarbi vooluallika energiat ning et ahelas toimub generaatori ja ahela vahel energiavahetusprotsess.

Analüüsime nüüd, kuidas on lood sellise skeemi tarbitava võimsusega.

Vahelduvvooluahelas tarbitav võimsus on võrdne voolu ja pinge korrutisega, kuid kuna vool ja pinge on muutuvad suurused, siis on ka võimsus muutuv.Sellisel juhul saame määrata iga ajahetke võimsuse väärtuse, kui korrutada voolu väärtus antud ajahetkele vastava pinge väärtusega.

Võimsuse graafiku saamiseks peame korrutama sirgjooneliste segmentide väärtused, mis määravad voolu ja pinge erinevatel aegadel. Selline konstruktsioon on näidatud joonisel fig. 3, a. Katkendlik lainekuju p näitab meile, kuidas võimsus muutub ainult induktiivset takistust sisaldavas vahelduvvooluahelas.

Selle kõvera koostamisel kasutati järgmist algebralise korrutamise reeglit: positiivse väärtuse korrutamisel negatiivse väärtusega saadakse negatiivne väärtus ja kahe negatiivse või kahe positiivse väärtuse korrutamisel saadakse positiivne väärtus.

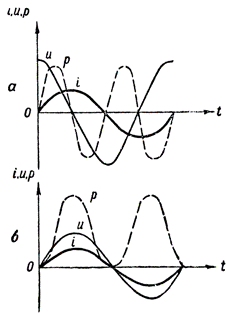
Joonis 3. Võimsuse graafikud: a — induktiivtakistust sisaldavas vooluringis, b — ka aktiivtakistus

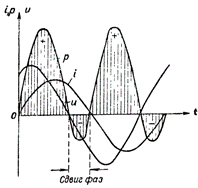
Joonis 4. R ja L sisaldava vooluahela võimsusgraafik.

Võimsuskõver asub sel juhul ajatelje kohal. See tähendab, et generaatori ja vooluringi vahel ei toimu energiavahetust ning seetõttu kulub generaatori poolt vooluringile antud võimsus täielikult vooluringile.

Joonisel fig. 4 on näidatud nii induktiivset kui ka aktiivtakistust sisaldava vooluahela võimsusgraafik. Sel juhul toimub ka energia pöördülekanne ahelast vooluallikasse, kuid palju vähemal määral kui ühe induktiivse takistusega ahelas.

Pärast ülaltoodud võimsusgraafikute ülevaatamist järeldame, et ainult voolu ja pinge vaheline faasinihe ahelas loob "negatiivse" võimsuse.Sel juhul, mida suurem on faasinihe voolu ja pinge vahel vooluringis, seda vähem energiat vooluahel tarbib ja vastupidi, mida väiksem on faasinihe, seda suurem on vooluringi tarbitav võimsus.

Loe ka: Mis on pingeresonants