Kütteelemendi arvutamine

Kütteelemendi traadi ühe peamise parameetri - läbimõõdu d, m (mm) - määramiseks kasutatakse kahte arvutusmeetodit: vastavalt lubatud eripinnavõimsusele PF ja voolukoormuste tabeli abil.

Lubatud eripinnavõimsus PF= P⁄F,

kus P on traatküttekeha võimsus, W;

F = π ∙ d ∙ l — küttekeha pindala, m2; l - traadi pikkus, m.

Esimese meetodi järgi

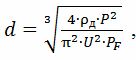
kus ρd — traadi materjali elektritakistus tegelikul temperatuuril, Ohm • m; U on küttekeha juhtme pinge V; PF - eripinna võimsuse lubatud väärtused erinevatele kütteseadmetele:

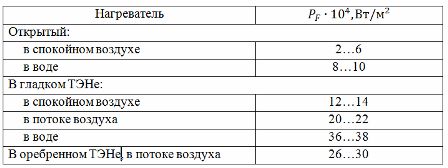
Teise meetodi puhul kasutatakse katseandmete põhjal koostatud voolukoormuste tabelit (vt tabel 1). Näidatud tabeli kasutamiseks on vaja arvutada küttetemperatuur Tp, mis on seotud juhi tegeliku (või lubatud) temperatuuriga Td suhtega:

Tr = Km ∙ Ks ∙ Td,

kus Km on paigaldustegur, võttes arvesse küttekeha jahutustingimuste halvenemist selle konstruktsiooni tõttu; Kc on keskkonnategur, arvestades küttekeha jahutustingimuste paranemist võrreldes statsionaarse õhukeskkonnaga.

Spiraalselt keeratud traadist valmistatud kütteelemendi puhul Km = 0,8 … 0,9; sama, keraamilise alusega Km = 0,6 ... 0,7; kütteplaatide ja mõne kütteelemendi traadi jaoks Km = 0,5 ... 0,6; elektripõrandast, pinnasest ja kütteelementidest pärit juhi puhul Km = 0,3 ... 0,4. Väiksem väärtus Km vastab väiksema läbimõõduga küttekehale, suurem väärtus suuremale läbimõõdule.

Töötamisel muudes tingimustes kui vaba konvektsioon, võetakse õhuvoolu kütteelementideks Kc = 1,3 … 2,0; elementide puhul seisvas vees Kc = 2,5; veevoolus — Kc = 3,0 … 3,5.

Kui tulevase (projekteeritud) küttekeha pinge Uph ja võimsus Pf on seatud, siis selle vool (faasi kohta)

Iph = Pph⁄Uph

Vastavalt küttekeha arvutatud voolu väärtusele selle kuumutamise vajalikuks arvutatud temperatuuriks vastavalt tabelile 1 leitakse nikroomtraadi d vajalik läbimõõt ja traadi vajalik pikkus m küttekeha valmistamiseks. arvutatakse:

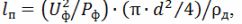
kus d on valitud traadi läbimõõt, m; ρd on juhi elektriline eritakistus tegelikul küttetemperatuuril, Ohm • m,

ρd = ρ20 ∙ [1 + αp ∙ (Td-20)],

kus αр — temperatuuri takistustegur, 1/OS.

Nikroomspiraali parameetrite määramiseks võtke keerdude keskmine läbimõõt D = (6 … 10) ∙ d, spiraali samm h = (2 … 4) ∙ d,

pöörete arv

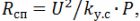
spiraali pikkus lsp = h ∙ n.

Kütteelementide arvutamisel tuleb meeles pidada, et spiraaltraadi takistus pärast kütteelemendi vajutamist

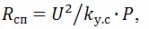
kus k (y.s) on koefitsient, mis võtab arvesse spiraali takistuse vähenemist; katseandmete järgi k (s) = 1,25. Arvestada tuleks ka sellega, et spiraaltraadi eripinnavõimsus on 3,5 ... 5 korda suurem torukujulise kütteelemendi pinna erivõimsusest.

Kütteelemendi praktilistes arvutustes määrake esmalt selle pinna temperatuur Tp = To + P ∙ Rt1,

kus See on ümbritseva õhu temperatuur, ° C; P on kütteelemendi võimsus W; RT1 - toru soojustakistus - keskmine liides, ОC / W.

Seejärel määratakse mähise temperatuur: Tsp = To + P ∙ (Rt1 + Rt2 + Rt3),

kus Rt2 on toru seina soojustakistus, ОC / W; RT3 — täiteaine soojustakistus, ОC / W; Rp1 = 1⁄ (α ∙ F), kus α on soojusülekandetegur, W / (m ^ 2 • ОС); F - küttekeha pindala, m2; Rt2 = δ⁄ (λ ∙ F), kus δ on seina paksus, m; λ — seina soojusjuhtivus, W / (m • ОС).

Lisateavet kütteelementide seadme kohta leiate siit: Kütteelemendid. Seade, valik, töö, kütteelementide ühendamine

Tabel 1. Voolukoormuste tabel

Näide 1. Arvutage elektriline küttekeha traatspiraali kujul vastavalt lubatud eripinnavõimsusele PF.

Seisund.Küttekeha võimsus P = 3,5 kW; toitepinge U = 220 V; traadi materjal — nikroom Х20Н80 (20% kroomi ja 80% nikli sulam), seetõttu traadi elektriline eritakistus ρ20 = 1,1 ∙ 10 ^ ( — 6) Ohm • m; temperatuuri takistustegur αр = 16 ∙ 10 ^ (- 6) 1 /ОС; spiraal on avatud, metallilisel kujul, spiraali töötemperatuur on Tsp = 400 ОC, PF= 12 ∙ 10 ^ 4 W / m2. Määrake d, lp, D, h, n, lp.

Vastus. Mähise takistus: R = U ^ 2⁄P = 220 ^ 2⁄3500 = 13,8 oomi.

Elektriline eritakistus Tsp = 400 OS juures

ρ400 = 1,1 ∙ 10 ^ (- 6) ∙ [1 + 16 ∙ 10 ^ (- 6) ∙ (400-20)] = 1,11 ∙ 10 ^ (- 6) oomi • m.

Leidke traadi läbimõõt:

Avaldisest R = (ρ ∙ l) ⁄S saame l⁄d ^ 2 = (π ∙ R) ⁄ (4 ∙ ρ), kust traadi pikkus

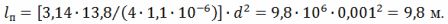
Spiraalpöörde keskmine läbimõõt on D = 10 ∙ d = 10 ∙ 0,001 = 0,01 m = 10 mm. Spiraali samm h = 3 ∙ d = 3 ∙ 1 = 3 mm.

Spiraali keerdude arv

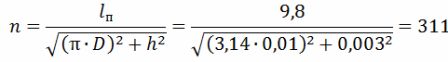
Heeliksi pikkus on lsp = h ∙ n = 0,003 ∙ 311 = 0,933 m = 93,3 cm.

Näide 2. Struktuurselt arvutage traadi takistussoojendi traadi läbimõõdu d määramisel, kasutades voolukoormuste tabelit (vt tabel 1).

Seisund. Traatküttekeha võimsus P = 3146 W; toitepinge U = 220 V; traadi materjal — nikroom Х20Н80 ρ20 = 1,1 ∙ 10 ^ ( — 6) Ohm • m; αp = 16 ∙ 10 ^ (- 6) 1 / ℃; õhuvoolus paiknev avatud spiraal (Km = 0,85, Kc = 2,0); juhi lubatud töötemperatuur Td = 470 ОС.

Määrake traadi läbimõõt d ja pikkus lp.

Vastus.

Tr = Km ∙ Ks ∙ Td = 0,85 ∙ 2 ∙ 470 OS = 800 OS.

Küttekeha arvutuslik vool I = P⁄U = 3146⁄220 = 14,3 A.

Voolukoormuste tabeli järgi (vt tabel 1) Tр = 800 ОС ja I = 14,3 A korral leiame traadi läbimõõdu ja ristlõike d = 1,0 mm ja S = 0,785 mm2.

Traadi pikkus lp = (R ∙ S) ⁄ρ800,

kus R = U ^ 2⁄P = 220 ^ 2⁄3146 = 15,3 oomi, ρ800 = 1,1 ∙ 10 ^ (- 6) ∙ [1 + 16 ∙ 10 ^ (- 6) ∙ (800-20) 1 = 20. 10 ^ (- 6) oomi • m, lp = 15,3 ∙ 0,785 ∙ 10 ^ (- 6) ⁄ (1,11 ∙ 10 ^ (- 6)) = 10,9 m.

Samuti saab vajadusel sarnaselt esimesele näitele defineerida D, h, n, lsp.

Näide 3. Määrake torukujulise elektrikerise (TEN) lubatud pinge.

Seisukord... Kütteelemendi mähis on valmistatud nikroomtraadist läbimõõduga d = 0,28 mm ja pikkusega l = 4,7 m Kütteelement on vaikses õhus, mille temperatuur on 20 °C. Nikroomi omadused: ρ20 = 1,1 ∙ 10 ^ (- 6) Ohm • m; αр = 16 ∙ 10 ^ (- 6) 1 / ° C. Kütteelemendi korpuse aktiivse osa pikkus on La = 40 cm.

Kütteelement on sile, välisläbimõõt dob ​​= 16 mm. Soojusülekandetegur α = 40 W / (m ^ 2 ∙ ° C). Soojustakistus: täiteaine RT3 = 0,3 ОС / W, korpuse seinad Rт2 = 0,002 ОС / W.

Määrake, millist maksimaalset pinget saab kütteelemendile rakendada, et selle mähise temperatuur Tsp ei ületaks 1000 ℃.

Vastus. Kütteelemendi kütteelemendi temperatuur

Tsp = To + P ∙ (Rt1 + Rt2 + Rt3),

kus See on ümbritseva õhu temperatuur; P on kütteelemendi võimsus W; RT1 — toru-keskkonna liidese kontaktsoojustakistus.

Kütteelemendi võimsus P = U ^ 2⁄R,

kus R on küttespiraali takistus.Seetõttu saame kirjutada Tsp-To = U ^ 2 / R ∙ (Rt1 + Rt2 + Rt3), kust tuleneb kütteelemendi pinge

U = √ ((R ∙ (Tsp-To)) / (Rt1 + Rt2 + Rt3)).

Leidke R = ρ ∙ (4 ∙ l) ⁄ (π ∙ d ^ 2),

kus ρ1000 = ρ20 ∙ [1 + αp ∙ (T-20)] = 1,1 ∙ 10 ^ (- 6) ∙ [1 + 16 ∙ 10 ^ (- 6) ∙ (1000-20)] = 1. — 6) Ohm • m.

Siis R = 1,12 ∙ 10 ^ (- 6) ∙ (4 ∙ 4,7) ⁄ (3,14 ∙ (0,28 ∙ 10 ^ (- 3)) ^ 2) = 85,5 oomi.

Kontakti soojustakistus RT1 = 1⁄ (α ∙ F),

kus F on kütteelemendi kesta aktiivse osa pindala; F = π ∙ dob ∙ La = 3,14 ∙ 0,016 ∙ 0,4 = 0,02 m2.

Leidke Rt1 = 1⁄ (40 ∙ 0,02 = 1,25) OC / W.

Määrake kütteelemendi pinge U = √ ((85,5 ∙ (1000-20)) / (1,25 + 0,002 + 0,3)) = 232,4 V.

Kui kütteelemendil näidatud nimipinge on 220 V, on ülepinge Tsp = 1000 OS juures 5,6% ∙ Un.