Kaod ja pingelangused – millised on erinevused

Tavalises inimelus kasutatakse sõnu "kaotus" ja "kukkumine" teatud saavutuste vähenemise fakti tähistamiseks, kuid need tähendavad teistsugust väärtust.

Sel juhul tähendab «kaod» osa kaotust, kahjustumist, varem saavutatud taseme suuruse vähendamist. Kaotused on ebasoovitavad, kuid võite neid taluda.

Sõna "kukkumine" mõistetakse kui tõsisemat kahju, mis on seotud õiguste täieliku äravõtmisega. Seega võivad isegi aeg-ajalt tekkivad kahjud (näiteks portfell) aja jooksul kaasa tuua languse (näiteks materiaalse eluea tase).

Sellega seoses käsitleme seda küsimust seoses elektrivõrgu pingega.

Kuidas tekivad kaod ja pingelangud

Elekter kantakse õhuliinide kaudu pikkade vahemaade taha ühest alajaamast teise.

Õhuliinid on ette nähtud lubatud võimsuse edastamiseks ja on valmistatud teatud materjali ja sektsiooni metalljuhtmetest. Need loovad takistusliku koormuse takistuse väärtusega R ja reaktiivkoormusega X.

Vastuvõtupoolel see seisab trafoelektrienergia muundamine.Selle mähistel on aktiivne ja väljendunud induktiivne takistus XL. Trafo sekundaarpool alandab pinget ja edastab selle edasi tarbijatele, kelle koormus väljendub Z väärtusega ning on oma olemuselt aktiivne, mahtuvuslik ja induktiivne. See mõjutab ka võrgu elektrilisi parameetreid.

Elektriülekande alajaamale kõige lähemal asuva õhuliini toe juhtmetele rakendatav pinge ületab igas faasis ahela reaktiiv- ja aktiivtakistuse ning loob selles voolu, mille vektor kaldub kõrvale vooluahela vektorist. rakendatud pinge nurga φ võrra.

Pingete jaotuse olemus ja voolude vool piki joont sümmeetrilise koormusrežiimi jaoks on näidatud fotol.

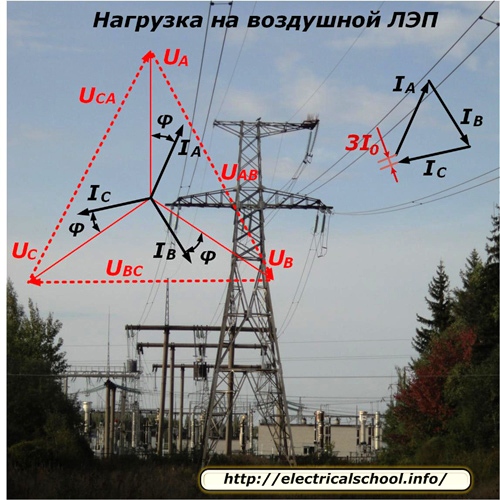
Kuna iga liini faas toidab erinevat hulka tarbijaid, kes on samuti juhuslikult lahti ühendatud või tööle ühendatud, on tehniliselt väga keeruline faasikoormust ideaalselt tasakaalustada. Selles on alati tasakaalustamatus, mille määrab faasivoolude vektorliit ja kirjutatakse 3I0. Enamikus arvutustes jäetakse see lihtsalt tähelepanuta.

Saatealajaama tarbitav energia kulub osaliselt liini takistuse ületamiseks ja jõuab vähese muutusega vastuvõtupoolele. Seda murdosa iseloomustab kadu ja pingelang, mille vektor amplituudilt veidi väheneb ja nihkub igas faasis nurga võrra.

Kuidas arvutatakse kadusid ja pingelangust

Elektri ülekandel toimuvate protsesside mõistmiseks on põhitunnuste kujutamiseks mugav vektorkuju. Sellel meetodil põhinevad ka erinevad matemaatilised arvutusmeetodid.

Arvutuste lihtsustamiseks kolmefaasiline süsteem seda esindab kolm ühefaasilist samaväärset ahelat. See meetod töötab hästi sümmeetrilise koormusega ja võimaldab analüüsida protsesse, kui see on katki.

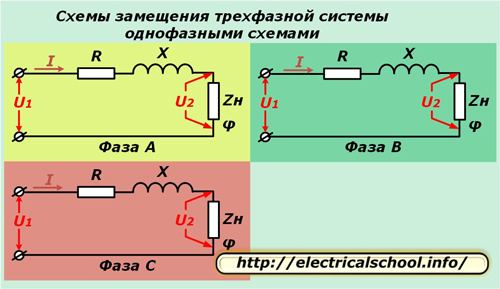
Ülaltoodud diagrammidel on liini iga juhi aktiivne R ja reaktants X ühendatud järjestikku komplekskoormuse takistusega Zn, mida iseloomustab nurk φ.

Lisaks teostatakse pingekao ja pingelanguse arvutamine ühes faasis. Selleks peate andmed täpsustama. Selleks valitakse energiat vastuvõttev alajaam, kus peab juba olema määratud lubatud koormus.

Iga kõrgepingesüsteemi pinge väärtus on juba teatmeteostes näidatud ning juhtmete takistused määratakse nende pikkuse, ristlõike, materjali ja võrgu konfiguratsiooni järgi. Maksimaalne vool vooluringis on seatud ja piiratud juhtmete omadustega.

Seetõttu on arvutuste alustamiseks: U2, R, X, Z, I, φ.

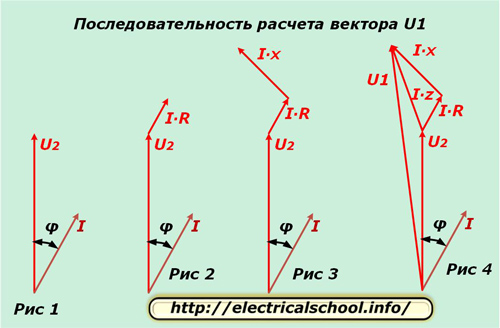
Võtame ühe faasi, näiteks «A» ja eraldame selle jaoks komplekstasandil vektorid U2 ja I, mis on nihutatud nurga φ võrra, nagu on näidatud joonisel 1. Juhi aktiivtakistuse potentsiaalne erinevus kattub suunas vooluga ja suurus määratakse avaldisega I ∙ R. Lükkame selle vektori U2 lõpust edasi (joonis 2).

Juhi reaktantsi potentsiaalne erinevus erineb voolu suunast nurga φ1 võrra ja arvutatakse korrutisest I ∙ X. Lükkame selle edasi vektorist I ∙ R (joonis 3).

Meeldetuletused: vektorite positiivse pöörlemissuuna korral komplekstasandil võetakse vastupäeva liikumine. Induktiivset koormust läbiv vool jääb rakendatud pingest nurga võrra maha.

Joonisel 4 on kujutatud potentsiaalsete erinevuste vektorite graafik juhtme kogutakistusest I ∙ Z ja pingest ahela U1 sisendis.

Nüüd saate võrrelda sisendvektoreid samaväärse ahelaga ja kogu koormusega. Selleks asetage saadud diagramm horisontaalselt (joonis 5) ja tõmmake algusest peale kaar mooduli U1 raadiusega kuni selle lõikumiseni vektori U2 suunaga (joonis 6).

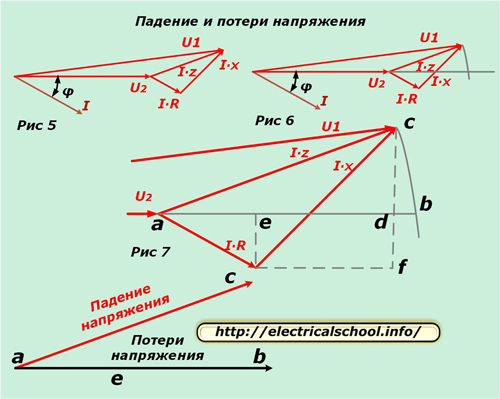
Joonisel 7 on näidatud kolmnurga suurendamine suurema selguse huvides ja abijoonte joonistamine, mis tähistab iseloomulikke tähtedega ristumispunkte.

Pildi allosas on näidatud, et saadud vektorit ac nimetatakse pingelanguks ja ab nimetatakse kaoks. Need erinevad suuruse ja suuna poolest. Kui pöördume tagasi algse skaala juurde, näeme, et ac saadakse vektorite geomeetrilise lahutamise tulemusena (U2 U1-st) ja ab on aritmeetiline. See protsess on näidatud alloleval pildil (joonis 8).

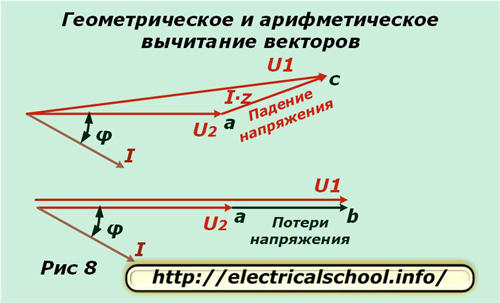
Pingekadude arvutamise valemite tuletamine

Nüüd pöördume tagasi joonise 7 juurde ja märkame, et bd segment on väga väike. Sel põhjusel jäetakse see arvutustes tähelepanuta ja pingekadu arvutatakse segmendi pikkuse ad järgi. See koosneb kahest joonelõigust ae ja ed.

Kuna ae = I ∙ R ∙ cosφ ja ed = I ∙ x ∙ sinφ, saab ühe faasi pingekadu arvutada valemiga:

∆Uph = I ∙ R ∙ cosφ + I ∙ x ∙ sinφ

Kui eeldame, et koormus on kõigis faasides sümmeetriline (tinglikult 3I0 tähelepanuta jättes), saame liini pingekadude arvutamiseks kasutada matemaatilisi meetodeid.

∆Ul = √3I ∙ (R ∙ cosφ + x ∙ sinφ)

Kui selle valemi parem pool korrutada ja jagada võrgupingega Un, siis saame valemi, mis võimaldab sooritada pArvutada pingekadusid läbi toiteallika.

∆Ul = (P ∙ r + Q ∙ x) / Un

Aktiivse P ja reaktiivvõimsuse Q väärtused saab võtta liiniarvesti näitude põhjal.

Seega sõltub pingekadu elektriahelas:

• vooluahela aktiivne ja reaktants;

• rakendatud võimsuse komponendid;

• rakendatud pinge suurus.

Pingelanguse põikkomponendi arvutamise valemite tuletamine

Läheme tagasi joonise 7 juurde. Vektori ac väärtust saab esitada täisnurkse kolmnurga acd hüpotenuusiga. Oleme reklaamijala juba välja arvutanud. Määrame põikkomponendi cd.

Joonisel on näha, et cd = cf-df.

df = ce = I ∙ R ∙ sin φ.

cf = I ∙ x ∙ cos φ.

cd = I ∙ x ∙ cosφ-I ∙ R ∙ sinφ.

Saadud mudelite abil teostame väikesed matemaatilised teisendused ja saame pingelanguse põikkomponendi.

δU = √3I ∙ (x ∙ cosφ-r ∙ sinφ) = (P ∙ x-Q ∙ r) / Un.

Pinge U1 arvutamise valemi määramine elektriliini alguses

Teades pinge väärtust sirge U2 lõpus, kadu ∆Ul ja languse põikkomponenti δU, saame Pythagorase teoreemi järgi arvutada vektori U1 väärtuse. Laiendatud kujul on sellel järgmine vorm.

U1 = √ [(U2 + (Pr + Qx) / Un)2+ ((Px-Qr) / Un)2].

Praktiline kasutamine

Pingekadude arvutamise viivad läbi insenerid elektriahela projekti loomise etapis võrgu ja selle koostisosade konfiguratsiooni optimaalseks valimiseks.

Elektripaigaldiste töötamise ajal saab vajadusel perioodiliselt läbi viia liinide otstes pingevektorite samaaegseid mõõtmisi ja võrrelda lihtsate arvutuste meetodil saadud tulemusi See meetod sobib seadmetele, mis on suurenenud nõuded tulenevalt suure töötäpsuse vajadusest.

Pingekaod sekundaarahelates

Näiteks võib tuua mõõtetrafode sekundaarahelad, mille pikkus ulatub mõnikord mitmesaja meetrini ja mida edastatakse spetsiaalse suurendatud ristlõikega toitekaabli abil.

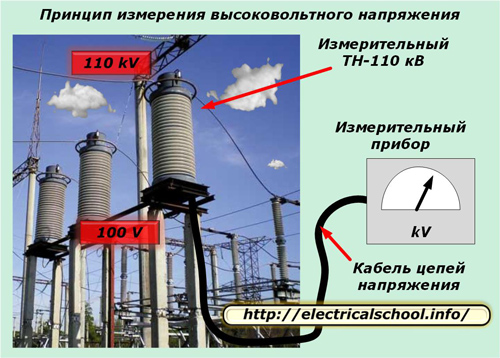
Sellise kaabli elektriliste omaduste suhtes kehtivad pinge ülekande kvaliteedi kõrgendatud nõuded.

Elektriseadmete kaasaegne kaitse eeldab kõrgete metroloogiliste näitajatega ja 0,5 või isegi 0,2 täpsusklassiga mõõtesüsteemide tööd. Seetõttu tuleb jälgida ja arvestada neile rakendatud pinge kadusid. Vastasel juhul võib nende seadmete töösse sisestatud viga oluliselt mõjutada kõiki tööomadusi.

Pingekaod pikkades kaabelliinides

Pika kaabli konstruktsiooni eripära on see, et sellel on mahtuvuslik takistus tänu juhtivate südamike üsna tihedale paigutusele ja õhukesele isolatsioonikihile nende vahel. See suunab edasi kaablit läbivat vooluvektorit ja muudab selle suurust.

I ∙ z väärtuse muutmise arvutamisel tuleb arvestada pingelanguse mõju mahtuvuslikule takistusele. Vastasel juhul ülalkirjeldatud tehnoloogia ei muutu.

Artiklis tuuakse näiteid elektriõhuliinide ja -kaablite kadudest ja pingelangustest. Neid leidub aga kõigis elektritarbijates, sealhulgas elektrimootorites, trafodes, induktiivpoolides, kondensaatorpankades ja muudes seadmetes.

Igat tüüpi elektriseadmete pingekadude suurus on töötingimuste osas seaduslikult reguleeritud ja nende määramise põhimõte on kõigis elektriahelates sama.